数据结构代码题思路汇总
P19
1:更新找到最小的值,固定这个位置的序号,然后交换即可
2:直接逆置即可
3:放在数值该在的位置上、移动到数值该在的位置上
4:放在数值该在的位置上、移动到数值该在的位置上
补充:计数排序思想也是把数值放在该放的位置上
5:放在该在的位置上比较容易理解
6:While,循环,将两边中比较小的给放在数组中,用三个数组下标即可,最后复制
7:全部逆置、前部分逆置、后部分逆置
8:有序表,先查,再决定操作;顺序或折半查找,然后找到交换,没找到插入
9:三个工作指针,小的向大的靠拢,当三者相同时打印并同时自增
10:全部逆置、前部分逆置、后部分逆置
11:设变量,X1、X2,A【X1】大,X2++,B【X2】大,X1++,While,条件X1+X2<N
最后判断A【X1】、B【X2】,哪个大哪个是中位数,本质是找X1+X2=N,找中间位置点
思想:小的向大的靠拢
最优解:折半,实现比较复杂
12:利用辅助数组存储对应值的出现次数,访问辅助数组查看是否有大于半数次数
利用题设条件:Ai<N,明显说明可以考虑用辅助数组
或者考虑先排序,然后统计相同元素出现的次数,若小于则清零向后统计不同的值
13:先快速排序,然后统计大于零的值是否符合递增标准变量的值,不等于直接跳出
根据跳出值的情况具体判断最小未出现正整数即可,建议列情况
14:设置三个下标变量,每次移动最小数值的下标,然后判断一次统计值
本质思想是,将范围收敛在最小的范围区域内,三指针思想
思想汇总:数放在该在的位置、多次逆置、多指针思想、小者向大者靠拢
高频代码命题点,但一般比较简单,若无最优解,向次优解考虑更佳
第二节
1:碰到符合条件的就删除
2:主扫描工作指针、辅前驱定位指针;或者冒泡转移结点到末尾,尾删
3:设置尾指针,头删、尾头插法;设置指向第一个结点的指针,后删、头部头插法
4:碰到符合条件的就删除
5:算出长度之差,然后设置同步指针,边走边比较,相同到一个就是公共结点
6:就地逆置,考虑设置尾指针、两个工作指针
7:后者与自身相同,删除后者
8:设置两个工作指针,小者向大者靠拢,碰到一样的就复制下来,共同移动一个位置
9:设置一个新链表,其他同上;或者直接在原有链表基础上修改(复杂)
10:设置一个主工作指针,两个辅工作指针,主用来衡量第一个,辅用来比较后续
11:两个工作指针,一个向前,一个向后,奇偶单独比较
12:断链、接链,保证正常循环即可
13:访问到该节点,更新相应内容,向前访问到插入位置,断链,插入
14:断链、全部插入头部即可
15:设置快慢指针,若两者相遇就必然存在环,甚至数学上还可以求解环的长度和起始
16:后半段依靠指针逆置,然后利用两个指针顺序相加
17:同步指针,同步,K个单位后再同步移动,一个走到末尾,一个就到对应位置
18:算法仅提及时间上的要求,因而可以采用数组存储,定下相同长度,再去访问即可
其余方法即为同步指针,先明确两者长,然后一个指针提前走,一个指针停顿后再走
边走边比较,走到相同的位置,就是公共部分的起始
19:算法仅明确时间的要求,因而考虑空间换时间,链表变为顺序表即容易操作
统计出现次数即可,然后遍历链表,如果这个值对应的次数不为一,删,再减,再判
20:后半段依靠指针逆置,设置两个工作指针,逐渐向后面断链、插入、移动
思想汇总:头插、尾插、同步指针、快慢指针、工作指针
统考命题重点,更多依靠命题角度去取巧,例如不要求时间、不要求空间,利用条件
命题中出现比较明显的提示也可以使用
代码题讲究的是经验,题目做得越多越容易反应出来怎么处理,时常回顾即可
P86
3:栈之间反复倒即可
4:思路有两种,一种不带空闲结点,一种牺牲一个空闲结点
实现而言牺牲更容易,对于此类题型,建议列举清楚从初始到一般的所有情况再写代码
复杂递归或者情况较多的时候,建议先列举情况,再写出对应处理代码
注:非统考命题重点,掌握循环队列的链式、顺序式即可
P158:
4:层序遍历的结果利用栈存储,最后一次性出栈
5:思想:利用层序遍历统计结点数,并向下遍历求其高度,可从此拓展衍生
二叉树高度的判断思想非常重要,建议细看
6:对二叉树进行层序遍历,把空结点也计入访问,如果碰到后还能访问到其他结点
说明这个树不是完全二叉树,因为按层序碰到一个空结点后就不能再有结点
7:设置全局变量,遍历一次二叉树,统计双分支结点的数量
8:遍历的时候同时进行交换,建议后序遍历
9:设置全局变量,遍历的同时修改变量值,等到变量值为零时利用全局变量存储其值
10:遍历一遍整个二叉树,建议后序遍历这样不会有冲突
访问到孩子节点为该值的根节点后,设置指针保存其孩子指针,然后置空该孩子
对该指针为根的子树进行一次后序遍历的删除操作即可
11:从根节点出发,设置一个工作指针,对工作指针指向的节点使用一次遍历
若遍历的结果是能够找到的,并且这个结点不是目标结点,就打印
那么就对指向节点的孩子使用遍历,判断哪个能够搜到目标,并且不是目标结点
将工作指针指向它,然后继续向下搜索即可,一路上就可以打印出这个祖先
本质是:祖先能够找到它,且两个孩子中只有一个孩子能找到它
12:接近上面的逻辑,从根结点出发,设置一个工作指针,指向对应的节点去搜索
如果这个节点能够搜索到两个结点,并且这个结点不是两者之一
那么就去考虑它的孩子,如果它的孩子不是两个结点之一,又能够找到两个
就把工作指针指向这个孩子,直到最终指向其中一个结点或者两个孩子都不能找到两个
本质是:共同祖先能够找到两个,单一祖先只能找到一个
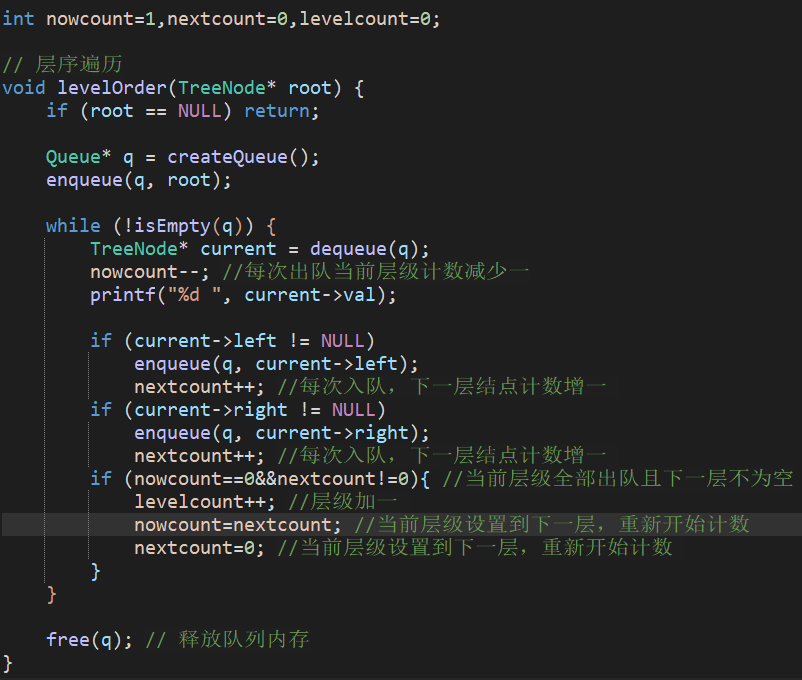
13:接近第五题的思路,设置本层计数、下层计数、最大层计数,略微改动代码
在更新每层计数的时候,顺便完成对每次结点数的计数更新
14:思想:每次去除第一个根的时候,后面都会划分为两段等长的左子树、右子树
对子树也可以同样进行划分,最终先打印左子、再打印右子,最后递归打印根
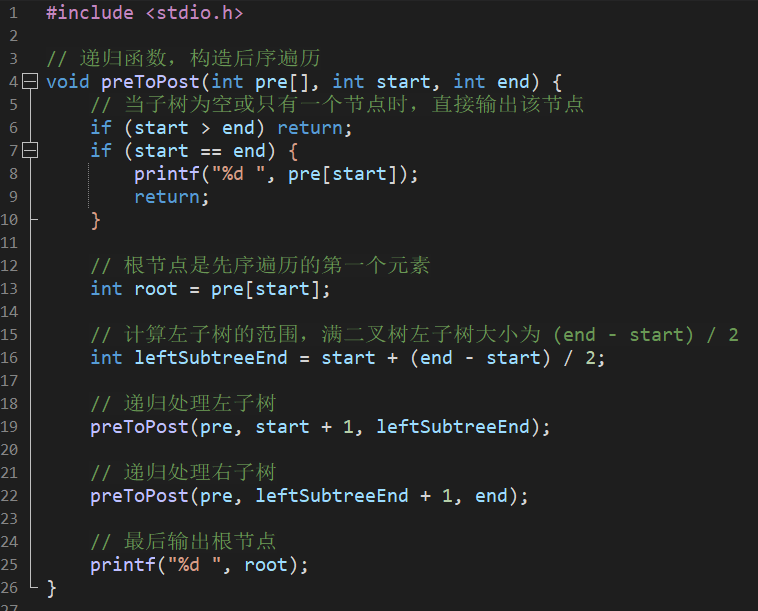
15:先序、中序、后序,均能够按顺序访问叶结点,因而可以任选一种
17:方法较多,一者考虑用非叶结点权值之和,一次遍历即可,一者考虑层级计算
int WPL;
void Travel(TreeNode* T, int deepth){
if(T!=NULL){
Travel(T->left,deepth+1);
Travel(T->right,deepth+1);
if(T->left==NULL&&T->right==NULL){
WPL=T->data*deepth+WPL;
}
}
}
18:中序遍历:左,根,右,那么只需要保证符号情况下输出:(左,根,右)
判断当前节点是否是操作符,是则需要打印括号,否则不需要打印
具体的打印过程:遍历左子树之前打印一个括号,遍历右子树结束后打印括号
// 中序遍历表达式树,并输出带括号的表达式
void printInOrder(TreeNode* root) {
if (root == NULL) return;
// 判断是否是操作符,如果是则需要加括号
int isOperator = !isalnum(root->val); // 非字母数字的是操作符
// 如果是操作符节点,开始左括号
if (isOperator) {
printf("(");
}
// 递归遍历左子树
printInOrder(root->left);
// 输出当前节点的值
printf("%c", root->val);
// 递归遍历右子树
printInOrder(root->right);
// 如果是操作符节点,结束右括号
if (isOperator) {
printf(")");
}
}
19:二叉排序树的判定,只要遍历一遍二叉树,递归判定每个结点是否符合定义即可
因为每个结点如果符合定义,整体一定是符合定义的,大小关系有传递性
思想汇总:层序遍历衍生、遍历判断、完全二叉树的判断、后序释放结点
祖先路径思想(从祖先遍历能找到)、子树分治划分、递归带参、树性质的传递性
二叉树高度判断的递归法
树的统考命题有一定递进强化的含义,因而需要重视关注递归遍历类型树算法
P185
4:正常遍历树,判定树的无左孩子节点的数量即可
5:求树深的代码都比较类型,其内容参考:P169、5,判定哪边的高度更高取高者
P198
2:本质是哈夫曼树的合并,试想:10、200;10、35,分别最大比较次数:200、35
因而每次应当和最小的合并,其实就是构造哈夫曼树
3:根据字符编码建立哈夫曼树,并为每个路径结点和叶结点都做标记区分
如果建树过程中遇到在叶节点后尝试建树的,直接说明不符合,一直没有说明符合
P204
1、2、3:递归返回、递归全局变量自增,两种思路
4:统计左子树高度、右子树高度,取最高的返回,比较推荐
6、9:随意遍历,中间加条件即可
8:递归返回、全局变量寻找,同样两种思路
7:层序遍历;10:依靠先序、层序配合形成输出值
拓展:
利用工作指针,指针指向拥有该树的子树根,逐渐缩小子树范围,直到指向节点
不足之处是时间复杂度较高,需要对每个祖先结点均进行一次遍历
总结:树算法的核心是利用递归函数值的返回或向下代,或者依靠递归函数求解
第三者一般是考场上的最优解,总体考察难度中等
P221
7:题干已经给出算法思想,即计算节点的度即可,注意审题,会错意会浪费大量时间
8:只需要遍历一遍计算结点的度即可,总体难度比较低
总结:统考在图算法命题上比较简单,一般仅考察邻接表、邻接矩阵、度的计算
P234
2:从某个节点开始广搜,在确认访问的时候修改访问位的含义,并做判断即可
3:无向连通图,若没有环那么就是一棵树,或者只有N-1条边也是树,根据此判断
环的判断:记录父结点,若下次访问结点不是父结点但已经被访问就存在环
4:从这个节点深搜、广搜,如果搜索到这个结点那么就确认有路径
5:思想是对每个邻接结点都调用一次深搜,并传递数组,若能达到则直接打印
并最终将目标结点给设置为未访问,这样就可以保证全部路径都能得到
其实和之前的工作指针思想也是类似的,不过这边的实现更为复杂,不是单纯的树状
深搜、广搜是图算法中比较容易考察的内容,以默写相应代码为基本目标
思想汇总:无向连通图的判断、环的判断、深搜的递归算法
P308
5:后序递归遍历即可,若每个结点都符合二叉排序树定义,整体就是二叉排序树
思想:利用树定义的递归性、传递性
6:每向下查找就是一层,因而查询过程本身就可以计数层级
7:引用类型的参数返回,最终会返回主调用函数,因而可以实现多参数返回
空树:平衡、高度为零;只有一个结点:平衡、高度为一
其他情况:高度取子树中最高者加一,平衡与否由子树是否平衡、高度差是否小于判断
本质上是树的遍历,无非是多添加几个判断和递归条件而已
8:中序给出第一个遍历的结点、最后一个遍历的结点即可
9:给出中序序列中的后一部分序列即可
10:列举情况,然后分别递归求解,重点在于列举清楚情况
Count1、Count2、Count3,作为根、左、右,三者各自所带的结点数
void Find(BiTree T,int k)
If count1=k // 根等于,找最右结点
FindRight(T)
If count1>k // 根大于,找孩子
If T->left!=NULL,Count2>k // 左子树大于,找左子树
Find(T-left,k)
If T->left!=NULL,Count2<k // 左子树小于,向右找结点
Find(T-right,k-count2)
If T->left!=NULL,Count2=k // 左子树同,找最右结点
FindRight(T-left)
If T->left!=NULL,Count3>k // 左子树不存在,找右子树
Find(T-right,k)
void FindRight(BiTree T)
While(T->right!=NULL) //找最右结点
T=T->Next
print(T-data)
注:上述代码仅是伪代码,以思想的角度呈现
注:此类算法题考察概率较低
P360
快排的思想:扫描法、分区与分治法
1:左右边分别扫描,扫描到对应的则交换
2:每次进行分区,基于中轴位置决定向前分区还是向后分区,折半思想
3:左右扫描,遇到对应的则交换;两趟总比较次数小于元素个数
4:每次进行分区,基于中轴位置决定向前还是向后进行分区,最终定位到目标
策略一:两边向中间扫描,交换
策略二:每次依靠分区算法定序基准并分区,通过中轴位置决定是否继续分区定基准
注:定基准可以定下目标元素最终的位序,划分元素为大于一端与小于一端
分治法:递归求解复杂问题,大区域划分为小区域,P158、18,类似的思想方法
注:以拓展思路为主,很少考察,或以最优解出现
P371
5:主工作指针用于定交换基准,辅助指针用于遍历查询、定位最小元素位置
6:排序树、平衡树、大根堆、小根堆,判断均可依靠传递性,各结点符合则整体符合
7:算法思想核心:若当前元素比最大的小,那么就插入相应的序列内
具体的实现可以用数组直接插入,或者采用大根堆反复调整,最终内部元素就是所得
注:算法题考察概率较低,可能会以简答题出现
拓展:分治法、贪心算法、动态规划、回溯法,可自行了解
分治法案例:折半查找、快速排序、归并排序
贪心算法:局部最优解求得全局最优解,最小生成树算法、最短路径算法

