PV模型:(有待整理汇总
对于书上基础算法较为形象的描述:
其实更应该说是一些较为经典的错误案例
单标志法:
如果现在没有轮到我用,我等
如果现在轮到我用
我用
下次给他用
评价:
这个算法的缺点其实比较明显的,如果下次他不用而我要用,那我就得一直等
更何况就算他用了也不一定考虑我用不用的问题,可能转手就把这个机会让给别人用了
极有可能会导致资源的浪费,甚至说长时间得不到使用导致的饥饿问题
违反了“空闲让进”,并且没有实现“让权等待”
其实核心就是,没有考虑到下次给他用的时候,他到底会不会用,以及会不会让给我用
双标志先检查法:
如果现在他想要用,那么给他用,我等
如果他现在不想用
那么我想用
我用
我用完了不想用了
评价:
这个算法同样存在漏洞
检查的时候他可能不想用,但是就在我设置想用的前那么几刻,他也想用了
而这时候我还没想用,他可能就会以为我不想用,于是我们两个一起想用,冲突了
简单来说就是两者检查均通过
违反了“忙则等待”,没有实现“让权等待”
核心是检查和设置中有一个间隔,这个间隔时间就会导致另一者的检查也通过
双标志后检查法:
我想用
如果他现在想用,那么给他用,我等
如果他现在不想用
我用
我用完了不想用了
评价:
这个算法就是在之前的状态改进了下,可以避免同时检查通过的情况
但依旧会有问题,在检查前两者可能都设置了想用,结果一检查的时候发现都想用
好好好我让你用,于是就互相谦让了半天谁都没有用,于是这下是真的要饥饿了
违反了“有限等待”,没有实现“让权等待”
核心是产生了死锁问题,互相谦让导致谁都没有成功
Peterson算法:
我想用
这轮让给他用
如果他现在想用并且这轮我们协商完了后让他先用
他用,我等
如果他现在不想用或者他想用但是我们协商完了后让我先用
我用
我用完了不想用了
评价:
对于协商过程以及后续的切换过程稍微做些解释,免得到时候看不懂
协商其实实际上是对轮数的设置,因为设置最终只有一个生效,所以不会产生一直谦让
同时在一个进程结束占用后,表达了自己不想用之后,其他进程的循环自然破解
其他都实现,唯独没有实现“让权等待”
硬件实现法:
关中断、开中断,单纯就是我执行的时候你不准来,你执行的时候我也不准来
TestAndSet:
测试资源当前是否上锁,不可访问
如果被上锁,不可访问,那么暂时等待
如果资源当前没有上锁,那么占用资源同时对资源上锁,使得其不可被其他访问
与Swap的区别在于这个封装了测试和上锁过程
Swap:
测试当前资源是否上锁,不可访问
如果被上锁,不可访问,那么暂时等待
如果资源当前没有上锁,那么占用资源同时对资源上锁,使得其不可被其他访问
与TestAndSet区别在于这个没有封装测试和上锁过程
Test和Swap均没有实现“让权等待”,因为其一直需要循环检查,互斥锁也是如此
和信号量的差别就在于信号量当占用资源检查失败时直接阻塞到等待队列,让出处理器
同时当别的进程释放资源的时候,唤醒一个进程
将原先古老而粗糙的反复敲门动作给细致化为没有资源不必反复追问
有资源的时候仅有可能是别的进程释放了资源,别的进程会唤醒进程,不需要主动追问
思想上是明显先进了的
互斥锁:
测试当前资源是否可用
如果不可用,那么暂时等待
如果可用,那么占据资源同时使得其不可用,不能被其他占据
信号量中,整型信号量中的wait当资源量小于等于零会一直测试所以没遵循“让权等待”
记录型信号量则实现了“让权等待”,因为其并没有循环
这里的资源,都设置为了物理意义,即资源数是多少,就代表还有多少资源
初始就是当前有的资源数
为0的时候就是当前没有资源了,为负一就是当前有一个预约了资源
整型信号量、记录型信号量:
整:
wait:
如果当前资源量不够,那么一直循环等待,反复追问(资源量小于等于0
其实说实话这边就算设置为等于0也没关系,因为不可能出现负数
如果当前资源量足够,那么占用一个资源(同时资源数量减一
signal:
释放自身占用的一个资源(资源数量加一
记录型:
wait:
先预约一个资源(资源量先减一
如果预约的资源目前被占据,那么进入阻塞队列等待(资源量小于0,主动阻塞
如果预约的资源目前没有被占据,那么占据该资源
signal:
释放自身占用的一个资源(资源量加一
如果资源被预约占据,那么从阻塞队列唤醒该进程(资源量小于等于0,被动唤醒
信号量实现互斥:
A:
P,如果没有别人占据(或,现在能得到这个资源,那么占据这个资源,并进入运行
如果别人占据或者说当前得不到这个资源,那么阻塞
V,释放该资源,可以让别人占据
B:
P,如果没有别人占据(或,现在能得到这个资源,那么占据这个资源,并进入运行
如果别人占据或者说当前得不到这个资源,那么阻塞
V,释放该资源,可以让别人占据
附:
简单来说就是对独占式资源的操作,资源只能被他人或者自己独占
要么你占,要么我占,要么谁都不占,只有一把椅子
信号量实现同步
P:如果现在能得到这个资源,那么占据这个资源并进入运行,否则就阻塞
V:创造出这个资源
附:
简单来说就是先得到了这个资源,再去消耗,没有这个资源,那么就先阻塞等待
主要是处理逻辑上的先后关系
前驱关系:
P1、P2、P3、P4、P5…..
如果现在能得到这些资源,那么占据这个资源并进入运行,否则就阻塞
V1、V2、V3、V4、V5…..
创造出这些资源
附:
本质是多同步问题,把上述的一个同步换为了多个同步问题
自然需要得到一系列的同步资源、条件后,才能占用资源并运行,否则就阻塞
当然其实个人认为,对于死锁的破解,一定要抓住一个想法:
至少让一个进程能够活动,完成运行
只要完成了这样一个操作,那么死锁自然也就不存在,自然就会被破解
类似的,只让四个哲学家吃饭,那么在这四个哲学家中至少有一个哲学家是正常吃饭的
因此就不可能产生死锁问题
银行家算法也是遵循了这个思想,每次至少让一个可行的进程先运行,而阻塞不可行的
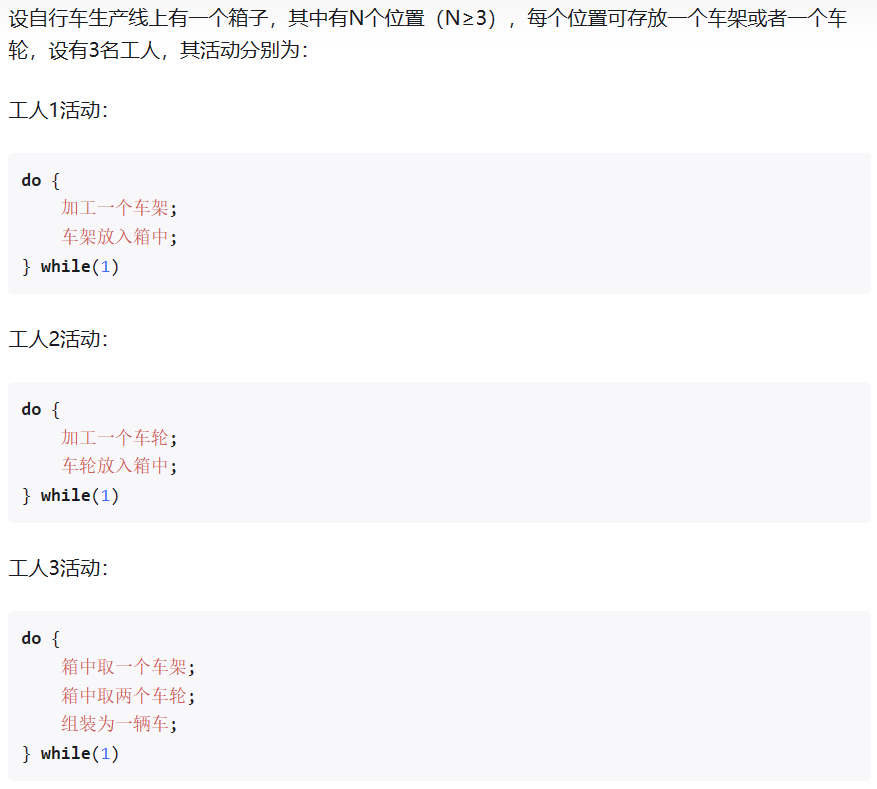
对于这个问题,也是类似的
需要避免的,就是箱子里全都是车轮或者全都是车架导致工人三无法组装的死锁问题
怎么避免?我想这种思路也是很容易看穿的
就是至少让当前箱子里,有那么一整套自行车的零部件
和死锁的处理思想几乎是一模一样,就是让当前至少能够正常完成一个进程
附:
参考代码:
semaphore mutex = 1; // 缓冲区互斥信号量
semaphore empty=N; // 箱子内的空位
semaphore weel=0; // 车轮
semaphore frame=0; // 车架
semaphore weel_empty=N-1; // 剩余车轮空位数名额
semaphore frame_empty=N-2; // 剩余车架空位数名额
工人1活动:
do {
加工一个车架;
P(frame_empty); // 占用缓冲区可放置车架数名额
P(empty); // 占用一个缓冲区空位置
P(mutex);
车架放入箱中;
V(mutex);
V(frame); // 车架数量+1
} while(1)
工人2活动:
do {
加工一个车轮;
P(weel_empty); // 占用缓冲区可放置车轮数名额
P(empty); // 占用一个缓冲区空位置
P(mutex);
车轮放入箱中;
V(mutex);
V(wheel); // 车轮数+1
} while(1)
工人3活动:
do {
P(frame); // 取出一个车架
P(mutex);
箱中取一个车架;
V(mutex);
V(empty); // 空位+1;
V(frame_empty); // 释放一个缓冲区可放置车架数名额;
P(wheel);
P(wheel);
P(mutex);
箱中取两个车轮;
V(mutex);
V(empty);
V(empty);
V(weel_empty); // 释放一个缓冲区可放置车轮数名额;
V(weel_empty); // 释放一个缓冲区可放置车轮数名额;
组装为一辆车;
} while(1)
其实这里引出一个问题,车轮、车架空位名额能否用计数量表示?
答案就是可以,但没什么必要
因为这里是一个工人只生产一种产品,所以即使是独占式的也不会导致其他工人无法工作
但,如果是多个工人生产一个产品,那么就一定要设置计数量,否则就会导致互斥
就会导致实际上只有一个工人在正常工作,别的工人都闲着,而实际上不应该有此逻辑
工人工作又不会是互斥的
但如果再稍微改一下,工人使用箱子是需要互斥的,应该怎么写?
这个就比较有趣,实际上应该在工人造完东西后再去申请这个箱子的使用权
而不是说工人在造东西的时候一直占用箱子,这就会导致各工人间的互斥
而实际需要的是工人之间能够并行工作,仅仅是打开放东西这一步需要互斥而已
算是一个比较有趣的变体,能准确模拟出来工作流程就能写
多生产者、单生产者、多消费者、单消费者、单一生产者资源,单一消费者资源
多生产者资源,多消费者资源,多口袋,口袋容量大于1,口袋容量等于一,排列组合
大多数都是消费者-生产者问题
[https://zhuanlan.zhihu.com/p/593795480]可搭配食用
生产者、消费者问题:
抽象为多生产者提供单一产品,多消费者消费单一产品,单口袋容量大于一的情况
对于生产者:
如果管道不满,并且能够得到管道使用权,那么写
对于消费者:
如果管道不空,并且能够得到管道使用权,那么读
构建逻辑关系:
互斥资源只有一个就是对管道的占据权
同步资源其实就是指当前的管道内的内容资源
下面有对这个资源进行解释,为何需要拆分为一个空,一个满而不是采用一个计数器
因而构建互斥资源初始量为一,两个同步资源一个初始量为零,一个初始量为满
需要先检查,后占用,否则会产生死锁问题
附:
可以更加简化流程
口袋空间设置为资源,口袋的使用权也设置为资源,消费者使用资源也设为资源
A当口袋没有生产者资源或者没有口袋使用权资源时陷入阻塞
A当口袋有生产者资源并且有口袋使用权时被唤醒并提供消费者资源、口袋使用权资源
唤醒的同时“消耗生产者资源”
P口袋有没有空资源(生产者资源
P口袋有没有人在用(口袋使用权
V创造口袋消费者资源
V口袋使用权
B当口袋没有消费者资源或者没有口袋使用权资源时陷入阻塞
B当口袋有消费者资源并且有口袋使用权时被唤醒并提供口袋使用权资源、生产者资源
唤醒的同时“消耗消费者资源”
P口袋有没有满资源(消费者资源
P口袋有没有人在用(口袋使用权
V创造口袋生产者资源
V口袋使用权
对于书上一长串话的解释:
简单来说就是导致了先占用,后检查,检查不通过,于是一直占用
对于生产者来说就是先占用了一个满的管道,然后检查发现是满的,于是一直不写
导致消费者想要读的时候被阻塞
对于消费者来说就是先占用了一个空的管道,然后检查发现是空的,于是一直不读
导致生产者想要写的时候被阻塞
其实这里就是典型的提示,必须要先检查有无生产者/消费者资源,再检查互斥量
否则会产生经典的死锁问题
附:
需要注意的是,这边采用了一个FULL和一个EMPTY两个变量来定义管道缓冲区状态
其实要理解为什么这里设置两个,因为没办法实现上限的控制
如果单纯使用一个X计数器,计数当前已经有的字数资源,那么实际上是达成不到效果的
因为用P、V操作,只能实现对X的占用、释放,无法对其设置一个上限,只能有个下限
计数器的话,是没办法实现互斥访问的,因为计数器资源只能代表字数资源
管道资源的占据,还是需要依靠一个互斥量来实现,计数器资源是一个同步资源
附:
其实这里对读、写两组进程,虽然说是一组,但因为实现了互斥资源的占用
所以实际上一时刻内只有一个进程在读或者写,而不是多个,Full和Empty资源是同步的
互斥资源只有那么一个,并且资源量从开始就固定不变,并且也是不允许被改变的
同步资源一般不止那么一个,资源量也随时都会改变
水果问题:
父亲而言:
如果当前盘子里没有水果,且母亲不放橘子,那么放一个苹果
母亲而言:
如果当前盘子里没有水果,且父亲不放苹果,那么放一个橘子
女儿而言:
如果当前盘子里有苹果,那么吃一个苹果
儿子而言:
如果当前盘子里有橘子,那么吃一个橘子
构建逻辑关系:
A当没有生产者资源或者没有使用权时陷入阻塞
A当有生产者资源并且有使用权时被唤醒消费生产者资源提供消费者资源
P有没有生产者资源(盘子是否为空
P口袋有没有人在用(盘子是否被占用
V创造消费者资源(提供一个苹果/橘子
V口袋使用权(口袋的互斥访问
B当没有消费者资源或者没有使用权时陷入阻塞
B当有消费者资源并且有使用权时被唤醒消费消费者资源提供生产者资源
P有没有消费者资源(盘子里是否有苹果/橘子
P口袋有没有人在用(盘子是否被占用
V创造生产者资源(提供一个空盘子
V口袋使用权(口袋的互斥访问
附:
其实可以看到书上的代码明显比我个人列出的更为简单和简洁
主要是删去了口袋使用权的互斥,其实也很容易理解
假设,口袋是有使用权的
生产者资源最多只有一个,意味着同一时刻只有一个生产者会占用该使用权
同时消费者在等待生产者创造消费者资源,不会过来占据口袋使用权
在逻辑上只需要实现,先释放口袋使用权,再创造消费者资源,就可以保证消费者不来用
同时因为生产者资源这时候已经用完了,在释放口袋使用权的时候也没生产者会用
消费者资源最多也只有一个,意味着同一时间也只有一个消费者会占用该使用权
同时生产者也类似,在等待消费者创造生产者资源,也不会过来占据口袋的使用权
在逻辑上,同样只需要实现,先释放口袋的使用权,再创造生产者资源,生产者也不会抢
可以看到这边的口袋使用权可以说是个摆设
生产者生产的时候,没有别人来占据,同时间只有一个生产者生产
消费者消费的时候,同样没有别人来占据,同时间只有一个消费者消费
所以没有这个互斥量也不会出事
但,个人列出的是更为广泛可用的一个模板,大部分消费者-生产者都可以这样处理
因为互斥往往在对共享资源的访问之上
生产者要等到有生产者资源的时候才能生产
消费者要等到有消费者资源的时候才能消费
同步、互斥量基本也就这些
读者、写者问题:
第一种思路,饿死写者思路
对于写者:
当现在没有读者在读并且写者在写的时候写
对于读者:
当现在没有写者在写的时候读
构建逻辑关系:
A当没有生产者资源的时候陷入阻塞,当没有访问权资源的时候阻塞
当有生产者资源的时候被唤醒,创造消费者资源
这里的生产者资源,就是指当前没有正在读的进程,若读进程为零则可用
这里的访问权资源,就是指当前没有正在写的进程,若有访问权资源则可用
在读者进程中采用锁写者资源的方式来决定是否有写者资源
因而实际上写者资源和访问权资源重复,同一时刻只能有一个写者资源
P写者资源
V写者资源
B当没有消费者资源的时候陷入阻塞
其他情况均创造生产者资源
这里的消费者资源,其实没有其他的,只有一个访问权资源,但多个读者又不互斥
所以肯定需要被写者互斥,但又不能对读者互斥,在读的时候内均锁住读者的写资源即可
这里的生产者资源,就是读者数量为零的时候创建,其他情况不创建
也可以采用一个读者计数器来实现创建
P互斥访问计数资源,这个必须互斥
readcount++
if readcount == 0
P锁住写者资源让其不能写
V互斥释放计数资源,当读的时候没必要占用资源,否则就会导致实际上变成单读者占用
P互斥访问计数资源,同样互斥修改计数器
readcount–
if readcount == 0
V释放写者资源让其现在能写
V互斥释放计数资源
第二种思路,写优先:
只需要补充一个读写互斥资源即可
写者占据资源的时候读者不能写,所以最后释放
读者占据资源的时候,主要是阻塞写者资源的情况下需要互斥,其他情况不需要
读者、写者问题的核心是采用了一个计数器,同时依赖计数器锁死写进程
当读者读的时候,只要有读者存在的情况,计数器都会保证写进程当前被锁死无法进行
当没有读者才释放让写者进行运行
保证了写者只有在当前读者全部退出的情况下才运行
同时也保证了当前的读者之间不会有互斥的访问
对计数器资源需要互斥访问,否则就会导致计数器表示的错误
吸烟者问题:
这个还是比较好理解的,其实就是生产者-消费者的变体,一个生产者提供多消费者资源
生产者而言
当有生产者资源的时候,当有占用权的时候
提供A或B或C,这个当前是需要随机数或者说顺序执行实现的
P生产者资源(这里是桌子是否空,或者说是否消费完
P占用权(这里是单生产者,所以不需要占用权,多生产者的时候需要考虑
对于消费者:
当有消费者资源,当有占用权的时候
消费A或B或C
P消费者资源,这里就是单纯的指代消费者资源,和水果资源是如出一辙的
P占用权,这里生产者和消费者同样是被动互斥占用的,和水果基本类似,不需要考虑
但写了肯定不会算错
V生产者资源(这里是指消费完毕,当前桌子为空,提供空资源,或提供空消费资源
其实消费者、生产者这边可以有非常多的变体
但个人认为,核心是把握生产者什么时候被阻塞,什么时候被唤醒生产,生产什么
对应,生产者资源、存储区占用权、消费者资源
消费者就是把握什么时候被阻塞,什么时候被唤醒消费,提供什么生产者资源
对应,消费者资源、存储区占用权、生产者资源
通过同步解决生产、消费资源
通过互斥解决存储区的占用权问题
非消费者-生产者问题:
哲学家问题:
一个进程需要同时持有多个临界资源,而这个临界资源可能被其他同类进程使用
于是就可能导致持有到一半的时候,另外一个也持有到一半,导致死锁
应该怎么处理?
其实最核心的就是,让一个哲学家现在能够吃饭
那么说实话如果不考虑系统量,我每次只让一个哲学家吃饭都没事,谁都只能看着他吃
当然没必要这样,互斥量就是基于这样一个思想提出的
先说书上的采用互斥量的解决方法
其实相当于每次只放一个哲学家进来取筷子,如果没有办法两个都取到那么就先等待
通过信号量mutex对eat()之前的取左侧和右侧筷子的操作进行保护,使之成为一个原子操作,防止死锁的出现
当一个哲学家两个筷子都取到后,那么就可以让别的哲学家取筷子,自己就先吃饭
这个适用性最广
再说,只放四个哲学家进来,让一个哲学家在外面饿着
其实这样就是保证一定会有一个哲学家当前能够成功进餐,其他的只需要等待就行
如果要普遍化的话,就是要实现“一次必须要有一个进程能够成功运行,且不会死锁”
奇数偶数、左右手撇子法都是一样的
保证当前一定有一个哲学家能够吃到饭,这就是核心

